Question

The number of nails of a given length is normally distributed with a mean length of 5 in and a standard deviation of 0.03 find the number of nails in a bag of 120 that are over 5.03 in long

Answer 1

19 nails

Explanation:

Let's first determine the z-score by using the formula:

`z=(x-\mu)/(\sigma)`

Where x=5.03, μ=5, σ=0.03 and so:

`z=(5.03-5)/(0.03)=1`

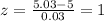
We can now use a z-score table to determine that 1.00 is synonymous with 0.8413 meaning 84.13%. This means that 84.13% of the nails are less than or equal to 5.03 inches long. Therefore, since we know 100% = 1 in decimals we can determine that the length greater than 5.03 inches is 1-0.8413=0.1587. This means that 15.87% of the 120 nails are greater than 5.03 inches long.

Finally, we can determine how many nails are greater than 5.03 by determining what is 15.87% of 120 which is:

`120 * 0.1587 \approx 19`

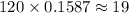
And so 19 out of the 120 nails are greater than 5.03 inches long.