Answer: There is probability of 0.57 chances that exactly three students from a group of four students have not passed Exam P/1 or Exam FM/2.
Explanation:
Total number of students = 8
Number of student who has passed Exam P/1 = 1
Number of student who has passed Exam FM/2 = 1
No student has passed more than one exam.
According to question, exactly three students from a randomly chose group of four students have not passed Exam P/1 or Exam FM/2.
So, Probability will be
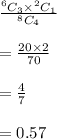
Hence, there is probability of 0.57 chances that exactly three students from a group of four students have not passed Exam P/1 or Exam FM/2.