Question

Which ordered pair is in the solution set of the system of linear inequalities? y >3/2 x – 1 y < 3/2x – 1

(–5, 2)

(2, 2)

(5, 2)

no solution

Answer 1

D. No solution

Explanation:

We are given the system of equations as,

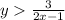`y>(3)/(2x-1)` and
`y<(3)/(2x-1)`.

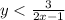It is required to find the solution of the given system.

As we have that,

`y>(3)/(2x-1)`

`y<(3)/(2x-1)`.

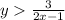
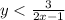i.e. the values of y are strictly greater than
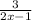`(3)/(2x-1)` and strictly less than
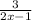`(3)/(2x-1)`, no region will be a common part of the solution.

Also, it can be seen in the graph below that there does not exist any common solution of this system as there is dotted line that is dividing the regions.

Hence, no solution is the correct option.

Answer 2

The correct option is 4.

Explanation:

The given inequalities are

`y>(3)/(2)-1` .... (1)

`y<(3)/(2)-1` .... (2)

From the given inequalities it is noticed that the related equation of both inequalities is

`y=(3)/(2)-1`

This line is dotted line because the sign of inequality is ">" and "<".

The shaded region of first inequality is upper side of the related line. The shaded region of second inequality is lower side of the related line.

Since there is no common shaded region, therefore the system of inequalities has no solution and option 4 is correct.