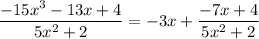We want to compute

The goal is to write it in the following form:
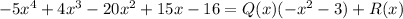
First step: How many "copies" of
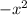 does
does
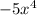 contain? We can write
contain? We can write
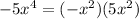 , so the answer is
, so the answer is
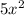 copies.
copies.
If we distribute
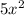 to
to
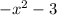 , we get
, we get
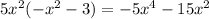
If we were done, then this product would have matched the numerator at the start. But it doesn't; there are still some terms that need to vanish. In particular, we still have to account for
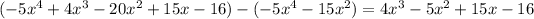
Second step: How many copies of
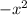 can we find in
can we find in
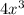 ? Well,
? Well,
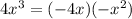 , so the answer is
, so the answer is
 . Then
. Then
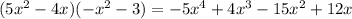
but this still doesn't match the original numerator. We still have to deal with

Third step: How many copies of
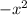 can we get out of
can we get out of
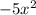 ?
?
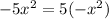 . Then
. Then
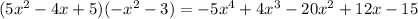
This also doesn't match the original numerator. We have a difference between what we have and what we want of
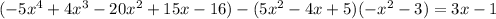
But we also can't divide
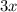 into chunks of
into chunks of
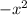 , and we can't continue the division algorithm.
, and we can't continue the division algorithm.
Our final answer would be

For the second problem, you should find