Question

The table has a set of equations that have arithmetic operations between rational and irrational numbers. Complete the table to find the sum. Then indicate whether the sum is rational or irrational.

Answer 1

1. rational

2.irrational

3.irrational

4.rational

5.rational

6.irrational

Explanation:

Answer 2

Explanation:

According to given equation

A =
`√(16) +(-(21)/(5))` ;
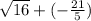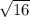`√(16)` can be simplified to 4.

Sum :
`√(16) +(-(21)/(5))` =
`(20-21)/(5) =-(1)/(5)`

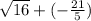4 is a rational number and
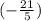`(-(21)/(5))` is also a rational number.

Sum of two rational number is always a rational number.

Therefore,
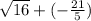`√(16) +(-(21)/(5))` is a rational number.

B = π+24 ; π is an irrational and 24 is a rational number.

Sum of an irrational and a rational is always a rational number.

Therefore, π+24 is an irrational number.

Sum = π+24

C =
`√(4) +5` ;
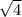`√(4)` can be simplified to 2.

2 is a rational number and 5 is also a rational number.

Sum = 2+5=7

Sum of two rational number is always a rational number.

Therefore,
`√(4) +5` is a rational number.

D =
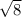`√(8)`+π ; π is an irrational and
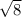`√(8)` is also an irrational number.

Sum =
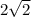`2√(2)`+π

Sum of two irrational number is always an irrational number.

Therefore,
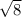`√(8)`+π is an irrational number.

E=
`√(36) +\sqrt[3]{27}`;
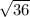`√(36)` can be simplified to 6 and
`\sqrt[3]{27}` can be simplified to 3.

6 is a rational number and 3 is also a rational number.

Sum = 6+3=9.

Sum of two rational number is always a rational number.

Therefore,
`√(36) +\sqrt[3]{27}` is a rational number.

F =
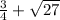`(3)/(4) +√(27)` ; \frac{3}{4} is a rational number and \sqrt{27} an irrational number.

Sum =
`(3)/(4) +3√(3)=(3+12√(3))/(4)`

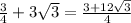
Sum of an irrational and a rational is always a rational number.

Therefore,
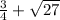`(3)/(4) +√(27)` is an irrational number.