Question

Suppose the invertible function φ(x) has the domain (−5,11) and the range (−12,1).

What is the range of φ^−1(x)?

Answer 1

The range of φ^−1(x) is: (-5,11)

Explanation:

We know that for any given function f(x) with the given domain and range.

If the function is invertible then the domain and range of the function and it's inverse get's interchanged.

i.e. the domain of the function is the range of it's inverse and the range of the function is the domain of it's inverse.

Here we have a invertible function φ(x) such that it has the domain (−5,11) and the range (−12,1).

This means that the range of it's inverse is: (-5,11)

Answer 2

Range of
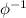`\phi^(-1)` is (−5,11).

Explanation:

Given the invertible function Ф(x) which has the domain (−5,11) and the range (−12,1).

Invertible function is the function that inverses another function i.e if y=Ф(x) then x=g(y) where g is called the inverse of Ф and denoted by
`\phi^(-1)`

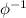
Given Ф(x) the function whose domain is (−5,11) and range is (−12,1). Therefore, by definition of invertible function there exist a function g with domain (−12,1) and range (−5,11) which is called the inverse function denoted by
`\phi^(-1)`

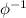
Hence, Range of
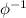`\phi^(-1)` is (−5,11)