Answer:
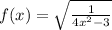 for
for
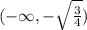 and
and
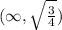 .
.
Explanation:
The given differential equation is
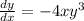
Rearranging it as
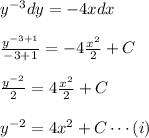
where C is constant.
The initial condition is f(-1)=-1, i.e for x=-1, y=-1.
So, by using the initial condition to get the value of constant:
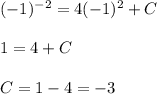
From equation (i), we have

As y=f(x), so the required particular solution
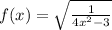
Now, determining the domain of the function
As for a real value output, the term under square root must be positive.
So,
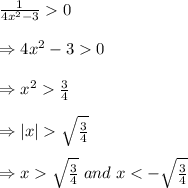
Therefore, the domain of the function is
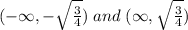
Hence,
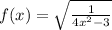 for
for
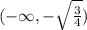 and
and
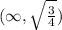 .
.