Question

Two lasers are shining on a double slit, with slit separation d. Laser 1 has a wavelength of d/20, whereas laser 2 has a wavelength of d/15. The lasers produce separate interference patterns on a screen a distance 5.20m away from the slits.

1. Which laser has its first maximum closer to the central maximum?
2. What is the distance Δymax--max between the first maxima (on the same side of the central maximum) of the two patterns?
3. What is the distance Δymax-min between the second maximum of laser 1 and the third minimum of laser 2, on the same side of the central maximum?

Answer 1

1) aser 1 has the maximum closest to the center

2) Δy = 0.0866 m , 3) Δy = 0.693 m

Step-by-step explanation:

The interference phenomenon is described by the expression

d sin θ = m λ for constructive interference

d sin θ = (m + ½) λ for destructive interference

We can use trigonometry to find the angle

tan θ = y / L

in trigonometry experiments the angles are small

tam θ =
`(sin \theta)/(cos \theta) = sin \theta`

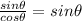
sin θ = y / L

we substitute

d y / L = m λ (1)

1) Let's find the first maximum that corresponds to m = 1 for each laser

laser 1 λ = d / 20

d y₁ / L = 1 d / 20

y₁ = L / 20

y₁ = 5.20 / 20

y₁ = 0.26 m

Laser 2 λ= d / 15

d y₂ / L = 1 d / 15

y₂ = d / 15

y₂ = 5.20 / 15

y₂ = 0.346 m

Therefore laser 1 has the maximum closest to the center

2) the difference between these maxima

Δy = y₂ - y₁

Δy = 0.3466 - 0.26

Δy = 0.0866 m

3) we look for the second maximum m = 2 of laser 1, we substitute in equation 1

y₃ = 2 5.20 / 20

y₃ = 0.52 m

now let's find the third minimum m = 3 of laser 2

d y₄ / L = (m + ½) λ

d y₄ / 5.20 = (3 + ½) d / 15

y₄ = 3.5 5.20 / 15

y₄ = 1.213 m

Δy = y₄ -y₃

Δy = 1.213 - 0.52

Δy = 0.693 m