Question

16

NOT TO
SCALE
The dagen sboas a circle, centre O.
AB is a chord of length 12 cm.
Vis the mid-point of 43 and OM = 45 cm
Calculate the radius of the circle.

Answer 1

7.5cm

lets take point K represent lenght from M to perimeter of circle.

r is radius

KM= r-OM= r-4.5cm

now lets draw line from O to A (OA)

we get triangle.

hypotenuse is OA and it equals r(radius)

ab=12 cm. so another side of the triangle (AM) is 12/2=6cm. and the last side of the triangle is 4.5(OM)

use pythaghorean theorem

squares of sides added = square of hypotenuse

20.25+36=r^2(our hypotenuse is radius)

56.25=r^2

r=√56.25=7.5cm

Answer 2

The radius of the circle is 7.5 cm

Explanation:

Circles and Lines

The figure provided shows a circle with two prominent features: a chord of length 12 cm and a segment from the center to the midpoint of the chord of length 4.5 cm.

We have attached an image with some additional measures to solve the problem.

Note a right triangle is formed with half the length of the chord (6 cm) and the distance from the center to the chord. We are sure the intersection divides the chord into two equal parts because M is its midpoint.

The radius of the circle is the hypotenuse of the triangle of legs 6 cm and 4.5 cm, thus the radius is:

`r=√(6^2+4.5^2)`

`r=√(36+20.25)`

`r=√(56.25)`

`\boxed{r = 7.5\ cm}`

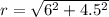
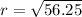
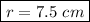
The radius of the circle is 7.5 cm