Question

the letters of the word independent are written on individual card and the cards are put into a box a card is selected and then replaced and then a second card is selected find the probality of obtaining​ the letter p twice

Answer 1

The probability of obtaining the letter p twice is 1/121

Explanation:

Probability of Recurring Events

There are 11 letters in the word 'independent', one of which is the letter 'p'.

When those letters are written on individual cards and they are put into a box, there are 11 different choices to pick at random.

This means the individual probability of getting a 'p' is:

`\displaystyle P_1=(1)/(11)`

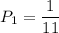
The card is reinserted into the box, leaving the sample space unaltered, thus the second card has the same probability:

`\displaystyle P_2=(1)/(11)`

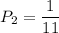
We'll use the multiplication rule. Just multiply the probability of the first event by the second.

`\displaystyle P=P_1*P_2=(1)/(11)*(1)/(11)`

`\displaystyle P=(1)/(121)`

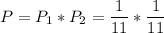
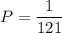
The probability of obtaining the letter p twice is 1/121