Question

A ball is moving with velocity 5 m/s in a direction which makes an angle of 30° with horizontal (i.e. with positive x-direction). This ball hits a vertical wall and gets reflected in a direction which makes an angle of 60° with the vertical (i.e. with positive y-direction) and moves with the same magnitude i.e. 5 m/s:

a. Find components of the initial and reflected velocities.
b. Show the vector representing the change in velocity of the ball.
c. Find the magnitude of the change in velocity.

Answer 1

Step-by-step explanation:

(a)

From the given information:

The initial velocity
`v_1` = 5 m/s

The direction of the angle θ = 30°

Therefore, the component along the x-axis =
`v_1 \ cos \ \theta`

`v_(1 \ x ) = 5 \ cos \ 30^0`

`v_(1x) = 4.33 \ m/s`

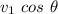
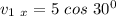
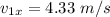
The component along the y-axis =
`v_2 { \ sin \ \theta}`

`v_(1 \ y ) = 5 \ sin \ 30^0`

`v_(1 \ y ) = 2.5 \ m/s`

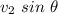
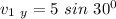
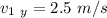
To find the final velocity( reflected velocity)

using the same magnitude
`v_2 = 5 \ m/s`

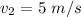
The angle from the x-axis can be
`\theta_r = 90^0+60^0`

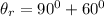
= 150°

Thus, the component along the x-axis =
`v_2 \ cos \theta _r`

`v_(2x) = - 0.433 \ m/s`

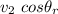
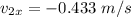
The component along the y-axis =
`v_2 \ sin \theta_r`

`v_(2y) = 5 \ sin \ 150^0`

`v_(2y) = 2.5 \ m/s`

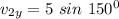
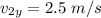
(b)

The velocity
`v_1` can be written as in vector form.

`v_1 ^(\to) = v_1 x \hat {i} + v_1 y \hat {j}`

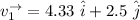`v_1 ^(\to) =4.33 \ \hat {i} + 2.5 \ \hat {j}` ---- (1)

The reflected velocity in vector form can be computed as:

`v_2 ^(\to) = v_2 x \hat {i} + v_2 y \hat {j}`

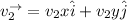
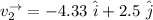`v_2 ^(\to) =-4.33 \ \hat {i} + 2.5 \ \hat {j}` --- (2)

The change in velocity =
`v_2 ^(\to) - v_1 ^(\to)`

`\Delta v ^(\to) = - 4.33 \hat i + 2.5 \hat j - 4.33 \hat i - 2.5 \hat j`

`\Delta v ^(\to) = - 8.66 \hat { i }`

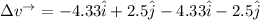
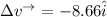
(c)

The magnitude of change in velocity =
`| \Delta V |`

`| \Delta V |` = 8.66 m/s