Question

10. A curve has the equation y = ax^3 + x + c, where a

and c are constants. The gradient of the curve at the
point (1, 2) is -2.
(i) Find the value of a and of c.
(ii) Hence, find the coordinates of the other point
on the curve where the gradient is -2.​

Answer 1

Part I)

`a=-1\text{ and } c=2`

Giving the equation:

`y=-x^3+x+2`

Part II)

(-1, 2)

Explanation:

We have the equation:

`y=ax^3+x+c`

Where a and c are constants.

We are given gradient/slope of the curve at the point (1, 2) is -2.

Part I)

We know that the gradient of the curve exactly at the point (1, 2) is -2.

So, we will differentiate our equation. We have:

`\displaystyle y=ax^3+x+c`

Differentiate both sides with respect to x:

`\displaystyle y^\prime=(d)/(dx)\big[ax^3+x+c\big]`

Expand the right:

`\displaystyle y^\prime=(d)/(dx)\big[ax^3]+(d)/(dx)\big[x\big]+(d)/(dx)\big[c\big]`

Since a and c are simply constants, we can move them outside:

`\displaystyle y^\prime=a(d)/(dx)\big[x^3]+(d)/(dx)\big[x\big]+c(d)/(dx)\big[1\big]`

Differentiate. Note that the derivative of a constant is simply 0.

`\displaystyle y^\prime=3ax^2+1`

We know that at the point (1, 2), the gradient/slope is -2.

Hence, when x is 1 and when y is 2, y’ is -2.

So (we don’t have a y so we can ignore it):

`-2=3a(1)^2+1`

Solve for a. Simplify:

`-2=3a+1`

Subtract 1 from both sides yield:

`-3=3a`

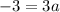
So, it follows that:

`a=-1`

Therefore, our derivative will be:

`y=-3x^2+1`

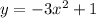
Now, we can go back to our original equation:

`y=ax^3+x+c`

Since we know that a is -1:

`y=-x^3+x+c`

Recall that we know that a point on our curve is (1, 2).

So, when x is 1, y is 2. By substitution:

`2=-(1)^3+1+c`

Solve for c. Simplify:

`2=-1+1+c`

Then it follows that:

`c=2`

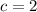
Hence, our entire equation is:

`y=-x^3+x+2`

Part II)

Our derivative is:

`y^\prime=-3x^2+1`

If the gradient is -2, y’ is -2. Hence:

`-2=-3x^2+1`

Solve for x. Subtracting 1 from both sides yields:

`-3=-3x^2`

So:

`x^2=1`

Then it follows that:

`x=\pm1\\`

Since we already have the point (1, 2) where x is 1, our other point is where x is -1.

Using our equation:

`y=-x^3+x+2`

We can see that our second point is:

`y=-(-1)^3+(-1)+2`

Simplify:

`y=1-1+2=2`

So, our second point where the gradient is -2 is at (-1, 2).