Question

g A proton and an alpha particle are released from rest at different locations from the negative plate of a charged parallel plate capacitor. The plates are 15 mm apart, and they are charged to a potential difference of 680 V. The alpha particle is placed at the point where the potential is 600 V. Where do you need to place the proton so that both particles reach the negative plate with the same speed

Answer 1

d₂ = 6.18 mm

Step-by-step explanation:

We can work on this interesting exercise using the concepts of energy conservation

alpha (1) particle, with have a charge q = 2e

Starting point

Em₀ = U = q V₁

final point

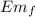`Em_(f)` = ½ m v²

Em₀ = Em_{f}

2eV₁ = ½ m₁ v²

v² =
`(4 \ e \ V_(1))/(m_(1) )`

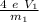
proton (2) particle, with have a charge q = e

Starting point

Em₀ = qV₂

Final point

Em_{f} = ½ m₂ v²

Em₀ = Em_{f}

eV₂ = ½ m₂ v²

v² =
`(2 \ e \ V_(2) )/(m_(2) )`

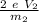
in the exercise, it should be noted that the two particles have the same velocity when reaching the plate, therefore let us solve the velocity in each equation and equal

\frac{4 \ e \ V_{1}}{m_{1} }= \frac{2 \ e \ V_{2} }{m_{2} }

`V_(2) = (2 m_(2) )/(m_(1) ) \ V_(1)`

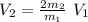
the alpha particle is composed of two protons and two neutrons, therefore in first approximation

m₁ = 4 m₂

subtitute

V₂ =
`(1)/(2)` V₁

let's calculate

V₂ =
`(1)/(2)` 600

V₂ = 300 V

To find the distance we use the relationship between the electric field and the potential difference

V = -d E

The electric field between the plates is constant, so

E = - V / d = - V₂ / d₂

d₂ =
`(V_(2) )/(V) \ d`

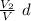
let's calculate

d₂ =
`(300)/(680) \ 15`

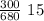
d₂ = 6.18 mm