Answer:
Part A)
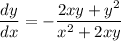
Part B)

Explanation:
We have the equation:
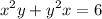
Part A)
We want to find the derivative of our function, dy/dx.
So, we will take the derivative of both sides with respect to x:
![\displaystyle (d)/(dx)\Big[x^2y+y^2x\Big]=(d)/(dx)\big[6\big]](https://img.qammunity.org/2021/formulas/mathematics/college/e1ixsjbzhky7d4dlp7ipq0xyxcmh32p20u.png)
The derivative of a constant is 0. We can expand the left:
![\displaystyle (d)/(dx)\Big[x^2y\Big]+(d)/(dx)\Big[y^2x\Big]=0](https://img.qammunity.org/2021/formulas/mathematics/college/sc1vhminnpsnbq0ntgwx37qvdy3j7dh1ig.png)
Differentiate using the product rule:
![\displaystyle \Big((d)/(dx)\big[x^2\big]y+x^2(d)/(dx)\big[y\big]\Big)+\Big((d)/(dx)\big[y^2\big]x+y^2(d)/(dx)\big[x\big]\Big)=0](https://img.qammunity.org/2021/formulas/mathematics/college/nbriu112hjcuxlm1ofnigvqhw9biyltd16.png)
Implicitly differentiate:

Rearrange:
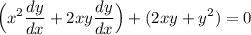
Isolate the dy/dx:
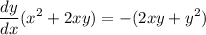
Hence, our derivative is:
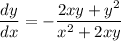
Part B)
We want to find the equation of the tangent line at (2, 1).
So, let's find the slope of the tangent line using the derivative. Substitute:
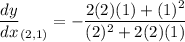
Evaluate:

Then by the point-slope form:

Yields:

Distribute:
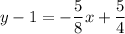
Hence, our equation is:
