Question

I need help, does anyone know how to simplify radical expressions?

Answer 1

`-2a\sqrt[3]{4a^2}`

Explanation:

`\sqrt[3]{-32a^5}\\\\=\sqrt[3]{-(2^5)a^5}\\\\=\sqrt[3]{(-1)^3(2^5)(a^5)}\\\\=\sqrt[3]{(-1)^3(2)^3(a)^3*2^2a^2}\\\\=-1*2*a*\sqrt[3]{4a^2}\\\\=-2a\sqrt[3]{4a^2}`

Answer 2

`-2a\sqrt[3]{4a^(2) } \\`

Explanation:

1) First, let's break down
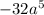`-32a^5` into its smallest factors:

`(-2) (-2) (-2) (-2) (-2) (a) (a) (a) (a) (a)`

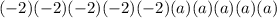
2) The 3 next to the radical indicates how many of the same kind of factors we need to group together in order to take that certain number or variable "out" of the radical. (It's a bit easier to understand if you look into the work shown below.) In this case, we need to group together the same kind of factors in groups of 3.

So, looking at the our factors, we can take out at least one group of (-2)s and one group of (a)s. Let's take them out of the radical like so:

`(-2) (a) \sqrt[3]{(-2)(-2)(a)(a) }`

3) From here, all you need to do is simplify and multiply back together:

`-2a\sqrt[3]{4a^2}`

This was a very short explanation, so if you have any questions on how to solve these kinds of problems, please do not hesitate to ask!