Help me pls: ∫cos ³(x)sin(x)dx

Question

asked Jul 9, 2021 179k views

1 Answer

Radbyx · Answer 1 · 2021-07-15T01:33:53+0000

Hello! :)

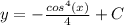
y = -(cos^(4)(x))/(4) + C

Use u-substitution to solve for the indefinite integral:

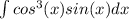
$\int cos^(3)(x)sin(x)dx$

Allow "u" to be the expression with an exponent:

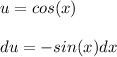
$u = cos(x)\\\\du = -sin(x)dx$

-du = sin(x)dx

In the integral, we are missing a negative symbol (du = -sin(x)), so we can adjust the integral to accommodate this.

Substitute "u" for cos(x) and du for -sin(x):

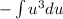
$-\int u^(3)du$

Use the integral power rule to solve:

$\int x^(n) = (x^(n + 1))/(n + 1)$

$-\int u^(3)du = -[(u^(4))/(4) ]$

Add the constant "C" as this is an indefinite integral:

= -[(u^(4))/(4) ] + C

Substitute in the value of u (cos(x)) into the equation:

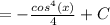
= -(cos^(4)(x))/(4) + C

And you're done!