Calculate the eccentricity of an ellipse. The distance between the foci is 5.2 and the length of the major axis is 20.6.Round off your answer to the nearest thousandths (0.000).…

Question

asked Aug 19, 2021 182k views

1 Answer

Janee · Answer 1 · 2021-08-25T12:28:42+0000

Answer:

The eccentricity of the ellipse is 0.252.

Step-by-step explanation:

The eccentricity of an ellipse (
), dimensionless, can be determined by means of the following expression:

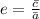$e = (\bar c)/(\bar a)$ (1)

Where:

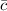$\bar c$ - Distance between the foci, dimensionless.

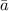$\bar a$ - Length of the major axis, dimensionless.

If we know that
$\bar c = 5.2$ and
$\bar a = 20.6$ , then the eccentricity of the ellipse is:

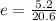
e = (5.2)/(20.6)

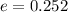
e = 0.252

The eccentricity of the ellipse is 0.252.