Answer:
Explanation:
The standard form of a circle is

If we are given x and y as 0 and 5 respectively, and we are also told that the center is (0, 0), our h and k are both 0. Filling in x, y, h, and k we can find the radius. So let's do that:
 and
and
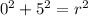 so
so
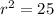 Our circle's equation is
Our circle's equation is
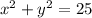
Since the point in question, (4, 4), lies in the first quadrant, we will concentrate on that quadrant only. To fall within the circle, we can set up an inequality and test the point (4, 4). If it lies ON the circle then the equality would be true. Let's try that first:

Obviously, 16 + 16 does not equal 25, so that point (4, 4) does not lie ON the circle. In fact from that statement alone, we can determine that the point lies outside the circle because
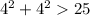
If the inequality < were true then the point would lie inside.