Answer:
The lower bound of a 99% C.I for the proportion of defectives = 0.422
Explanation:
From the given information:
The point estimate = sample proportion



 = 0.55
= 0.55
At Confidence interval of 99%, the level of significance = 1 - 0.99
= 0.01
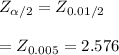
Then the margin of error
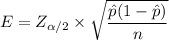
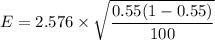
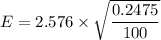
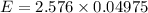
E = 0.128156
E ≅ 0.128
At 99% C.I for the population proportion p is:

= 0.55 - 0.128
= 0.422
Thus, the lower bound of a 99% C.I for the proportion of defectives = 0.422