Question

Find the dimensions of the rectangular box with maximum volume in the first octant with one vertex at the origin and the opposite vertex on the ellipsoid 4x^2+y^2+4z^2=4

a. The length of the box in the x-direction is:_______
b. The length of the box in the y-direction is:_______
c. The length of the box in the z-direction is:_______

Answer 1

Let x, y, z be the dimensions of the rectangle.

Volume of the rectangle (V) = xyz

Given that the vertex should lie on ellipse
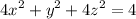`$4x^2 + y^2+4z^2=4$` .......(i)

So here the volume xyz must be maximum with constraints above.

We solve this using Lagranches method with variable λ

Lagranches function is

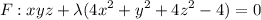`$F : xyz + \lambda(4x^2+y^2+4z^2-4)=0$` .....(ii)

To find λ,
`$(dF)/(dx)=0; (dF)/(dy)=0;(dF)/(dz)=0$`

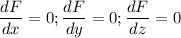
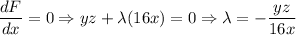`$(dF)/(dx)=0 \Rightarrow yz+\lambda(16x)=0 \Rightarrow \lambda = -(yz)/(16x)$` .............(iii)

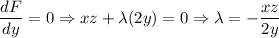`$(dF)/(dy)=0 \Rightarrow xz+\lambda(2y)=0 \Rightarrow \lambda = -(xz)/(2y)$` ..................(iv)

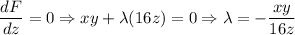`$(dF)/(dz)=0 \Rightarrow xy+\lambda(16z)=0 \Rightarrow \lambda = -(xy)/(16z)$` ...............(v)

Equating (iii) and (iv)

`$-(yz)/(16x)=-(xz)/(2y) \Rightarrow y^2=8x^2 \Rightarrow y = \sqrt8 x$` ...............(vi)

Equating (iii) and (v)

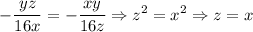`$-(yz)/(16x)=-(xy)/(16z) \Rightarrow z^2=x^2 \Rightarrow z = x$` ....................(vii)

Substitute (vi) and (vii) in (i),

From (i),

`$4x^2 + (\sqrt8 x)^2+4x^2 = 4$`

`$\Rightarrow 4x^2 +8x^2+4x^2 = 4 \Rightarrow x = (1)/(4)$`

From (vi),

`$y = \sqrt8 x$`

`$\Rightarrow y= \sqrt8 * (1)/(4) \Rightarrow y =(\sqrt8)/(4)$`

`$\Rightarrow y =(√(2*4))/(4) \Rightarrow y = (1)/(\sqrt2)$`

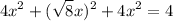
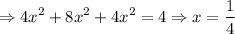
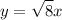
From (vii),

z = x

`$z =(1)/(4)$`

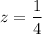
Therefore, for maximum volume the dimensions of a rectangle box are

`$x =(1)/(4) ; y = (1)/(\sqrt2) ; z =(1)/(4)$`