Question

How many distinct rearrangements of the letters in "sleepless" are there?

Answer 1

`N = 5040`

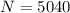
Explanation:

Required

Arrange the letters of "sleepless"

First, we count the number (n) of characters

`n = 9`

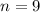
First, we count the number (n) of repeated characters

`s = 3`

`e = 3`

`l = 2`

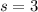
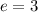
The arrangement (N) is then calculated as follows;

`N = (n!)/(s!e!l!)`

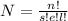
This gives:

`N = (9!)/(3!3!2!)`

`N = (9*8*7*6*5*4*3*2*1)/(3*2*1*3*2*1*2*1)`

`N = (362880)/(72)`

`N = 5040`

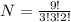
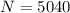
Hence, there are 5040 distinct arrangements