Question

Find f'(x) and state the domain of f':
f(x) = In (2x^2+1)

Answer 1

`f'(x) = (4x)/(2x^2+1)`

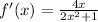
Domain: All Real Numbers

General Formulas and Concepts:

Algebra I

• Domain is the set of x-values that can be inputted into function f(x)

Calculus

The derivative of a constant is equal to 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Chain Rule:
`(d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Derivative:
`(d)/(dx) [ln(u)] = (u')/(u)`

Explanation:

Step 1: Define

f(x) = ln(2x² + 1)

Step 2: Differentiate

1. Derivative ln(u) [Chain Rule/Basic Power]:
   `f'(x) = (1)/(2x^2+1) \cdot 2 \cdot 2x^(2-1)`
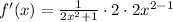
2. Simplify:
   `f'(x) = (1)/(2x^2+1) \cdot 4x`
3. Multiply:
   `f'(x) = (4x)/(2x^2+1)`

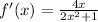
Step 3: Domain

We know that we would have issues in the denominator when we have a rational expression. However, we can see that the denominator would never equal 0.

Therefore, our domain would be all real numbers.

We can also graph the differential function to analyze the domain.