Prove the following integration formula: \displaystyle \int e^(au)\sin(bu)\, du=(e^(au))/(a^2+b^2)(a\sin(bu)-b\cos(bu))+C

Question

Prove the following integration formula:


`\displaystyle \int e^(au)\sin(bu)\, du=(e^(au))/(a^2+b^2)(a\sin(bu)-b\cos(bu))+C`

Answer 1

See Explanation.

General Formulas and Concepts:

Pre-Algebra

• Distributive Property
• Equality Properties

Algebra I

• Combining Like Terms
• Factoring

Calculus

• Derivative 1:
  `(d)/(dx) [e^u]=u'e^u`
• Integration Constant C
• Integral 1:
  `\int {e^x} \, dx = e^x + C`
• Integral 2:
  `\int {sin(x)} \, dx = -cos(x) + C`
• Integral 3:
  `\int {cos(x)} \, dx = sin(x) + C`
• Integral Rule 1:
  `\int {cf(x)} \, dx = c \int {f(x)} \, dx`
• Integration by Parts:
  `\int {u} \, dv = uv - \int {v} \, du`
• [IBP] LIPET: Logs, Inverses, Polynomials, Exponents, Trig

Explanation:

Step 1: Define Integral

`\int {e^(au)sin(bu)} \, du`

Step 2: Identify Variables Pt. 1

Using LIPET, we determine the variables for IBP.

Use Int Rules 2 + 3.

`u = e^(au)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = sin(bu)du\\du = ae^(au)du \ \ \ \ \ \ \ \ \ v = (-cos(bu))/(b)`

Step 3: Integrate Pt. 1

1. Integrate [IBP]:
   `\int {e^(au)sin(bu)} \, du = (-e^(au)cos(bu))/(b) - \int ({ae^(au) \cdot (-cos(bu))/(b) }) \, du`
2. Integrate [Int Rule 1]:
   `\int {e^(au)sin(bu)} \, du = (-e^(au)cos(bu))/(b) + (a)/(b) \int ({e^(au)cos(bu)}) \, du`

Step 4: Identify Variables Pt. 2

Using LIPET, we determine the variables for the 2nd IBP.

Use Int Rules 2 + 3.

`u = e^(au)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = cos(bu)du\\du = ae^(au)du \ \ \ \ \ \ \ \ \ v = (sin(bu))/(b)`

Step 5: Integrate Pt. 2

1. Integrate [IBP]:
   `\int {e^(au)cos(bu)} \, du = (e^(au)sin(bu))/(b) - \int ({ae^(au) \cdot (sin(bu))/(b) }) \, du`
2. Integrate [Int Rule 1]:
   `\int {e^(au)cos(bu)} \, du = (e^(au)sin(bu))/(b) - (a)/(b) \int ({e^(au) sin(bu)}) \, du`

Step 6: Integrate Pt. 3

1. Integrate [Alg - Back substitute]:
   `\int {e^(au)sin(bu)} \, du = (-e^(au)cos(bu))/(b) + (a)/(b) [(e^(au)sin(bu))/(b) - (a)/(b) \int ({e^(au) sin(bu)}) \, du]`
2. [Integral - Alg] Distribute Brackets:
   `\int {e^(au)sin(bu)} \, du = (-e^(au)cos(bu))/(b) + (ae^(au)sin(bu))/(b^2) - (a^2)/(b^2) \int ({e^(au) sin(bu)}) \, du`
3. [Integral - Alg] Isolate Original Terms:
   `\int {e^(au)sin(bu)} \, du + (a^2)/(b^2) \int ({e^(au) sin(bu)}) \, du= (-e^(au)cos(bu))/(b) + (ae^(au)sin(bu))/(b^2)`
4. [Integral - Alg] Rewrite:
   `((a^2)/(b^2) +1)\int {e^(au)sin(bu)} \, du = (-e^(au)cos(bu))/(b) + (ae^(au)sin(bu))/(b^2)`
5. [Integral - Alg] Isolate Original:
   `\int {e^(au)sin(bu)} \, du = ((-e^(au)cos(bu))/(b) + (ae^(au)sin(bu))/(b^2))/((a^2)/(b^2) +1)`
6. [Integral - Alg] Rewrite Fraction:
   `\int {e^(au)sin(bu)} \, du = ((-be^(au)cos(bu))/(b^2) + (ae^(au)sin(bu))/(b^2))/((a^2)/(b^2) +(b^2)/(b^2) )`
7. [Integral - Alg] Combine Like Terms:
   `\int {e^(au)sin(bu)} \, du = ((ae^(au)sin(bu)-be^(au)cos(bu))/(b^2) )/((a^2+b^2)/(b^2) )`
8. [Integral - Alg] Divide:
   `\int {e^(au)sin(bu)} \, du = (ae^(au)sin(bu) - be^(au)cos(bu))/(b^2) \cdot (b^2)/(a^2 + b^2)`
9. [Integral - Alg] Multiply:
   `\int {e^(au)sin(bu)} \, du = (1)/(a^2+b^2) [ae^(au)sin(bu) - be^(au)cos(bu)]`
10. [Integral - Alg] Factor:
    `\int {e^(au)sin(bu)} \, du = (e^(au))/(a^2+b^2) [asin(bu) - bcos(bu)]`
11. [Integral] Integration Constant:
    `\int {e^(au)sin(bu)} \, du = (e^(au))/(a^2+b^2) [asin(bu) - bcos(bu)] + C`

And we have proved the integration formula!

Answer 2

Prove:
`\displaystyle \int e^a^u sin(bu)\ du = (e^a^u)/(a^2+b^2) (a \ sin(bu) - b \ cos(bu)) + C`

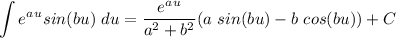
Integration by parts formula:
`\displaystyle \int udv = uv - \int vdu`

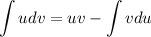
Find u, du, v, and dv for this function:
`\displaystyle \int e^a^u sin(bu)`

• 
  `\displaystyle u =e^a^u \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ v = -(cos(bu))/(b) \\ du=ae^a^u \ du \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = sin(bu) \ du`

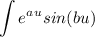
Plug these values into the IBP formula.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = e^a^u \cdot (-cos(bu))/(b) - \int -(cos(bu))/(b) \cdot ae^a^u \ du`

Multiply and simplify the factors. Factor the negative out of the integral.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = -(e^a^u cos(bu))/(b) +\int (a \ cos(bu) \ e^a^u)/(b) \ du`

Factor out a/b from the integral.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = -(e^a^u cos(bu))/(b) + (a)/(b) \int cos(bu) \ e^a^u \ du`

Now we are going to apply IBP to the function:
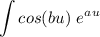`\displaystyle \int cos(bu) \ e^a^u` . Find u, du, v, and dv for this function.

• 
  `\displaystyle u =e^a^u \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ v = (sin(bu))/(b) \\ du=ae^a^u \ du \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = cos(bu) \ du`

Plug these values into the IBP formula.

• 
  `\displaystyle \int e^a^u cos(bu) \ du = e^a^u \cdot (sin(bu))/(b) - \int (sin(bu))/(b) \cdot ae^a^u \ du`

Multiply and simplify the factors.

• 
  `\displaystyle \int e^a^u cos(bu) \ du = (e^a^u \ sin(bu))/(b) - \int (a \ sin(bu)\ e^a^u)/(b) \ du`

Factor out a/b from the integral.

• 
  `\displaystyle \int e^a^u cos(bu) \ du = (e^a^u \ sin(bu))/(b) - (a)/(b) \int sin(bu)\ e^a^u} \ du`

Notice that we have the same integral we started with. Let's plug this integral into the original IBP we did.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = -(e^a^u cos(bu))/(b) + (a)/(b) \big{[ }(e^a^u sin(bu))/(b) - (a)/(b) \int sin(bu) \ e^a^u \ du \big{]}}`

Distribute a/b inside the parentheses.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = -(e^a^u cos(bu))/(b) + (a \ e^a^u sin(bu))/(b^2) - (a^2)/(b^2) \int sin(bu) \ e^a^u \ du`

Factor 1/b out of the right side of the equation.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = (1)/(b)\big{[} -e^a^u cos(bu)+ a \big{(}(e^a^u sin(bu))/(b) \big{)} - (a^2)/(b) \int sin(bu) \ e^a^u \ du \big{]}`

Multiply both sides by b to get rid of 1/b.

• 
  `\displaystyle b \int e^a^u sin(bu) \ du = -e^a^u cos(bu)+ a \big{(}(e^a^u sin(bu))/(b) \big{)} - (a^2)/(b) \int sin(bu) \ e^a^u \ du`

Add the integral to both sides of the equation.

• 
  `\displaystyle b \int e^a^u sin(bu) \ du + (a^2)/(b) \int sin(bu) \ e^a^u \ du= -e^a^u cos(bu)+ a \big{(}(e^a^u sin(bu))/(b) \big{)}`

Factor the integral on the left side.

• 
  `\displaystyle \int e^a^u sin(bu) \ du \ \big{(} b + (a^2)/(b) \big{)}= -e^a^u cos(bu)+ a \big{(}(e^a^u sin(bu))/(b) \big{)}`

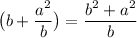`\displaystyle \big{(}b+(a^2)/(b) \big{)} = (b^2+a^2)/(b)`, so we can multiply both sides of the equation by
`\displaystyle (b)/(a^2+b^2)`.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = -e^a^u cos(bu)+ a \big{(}(e^a^u sin(bu))/(b) \big{)} \big{(} (b)/(a^2+b^2) \big{)}`

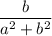Simplify the equation before multiplying everything by
`\displaystyle (b)/(a^2+b^2)`.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = \big{(}(-e^a^u cos(bu) \ b + a \ e^a^u sin(bu))/(b) \big{)} \big{(} (b)/(a^2+b^2) \big{)}`

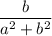Multiply the two factors together. Notice that the two b's in the denominator and numerator, respectively, cancel out. We are left with:

• 
  `\displaystyle \int e^a^u sin(bu) \ du = \big{(}(-e^a^u cos(bu) \ b + a \ e^a^u sin(bu))/(a^2+b^2) \big{)}`

Factor
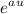`\displaystyle e^a^u` from the numerator.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = \big{(}(e^a^u( -b \ cos(bu) \ + a \ sin(bu))/(a^2+b^2) \big{)}`

Split the numerator and denominator to make it appear the same as the original question.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = (e^a^u)/(a^2+b^2) \big{(} a \ sin(bu) - b \ cos(bu) \big{)}`

Since we are taking the integral of something, we can add a +C at the end to complete the problem.

• 
  `\displaystyle \int e^a^u sin(bu) \ du = (e^a^u)/(a^2+b^2) \big{(} a \ sin(bu) - b \ cos(bu) \big{)} + C`

This is equivalent to the proof that we are given, therefore, we proved the integral correctly.