Question

Find the missing y-coordinate that makes the two triangles congruent. Triangle ABC: A(8,4), B(2,6), C(5, 0) Triangle MNO: M(7,4), N(1,2), O(4, y)

Answer 1

y = 8

Explanation:

Two triangles are said to be congruent if all the three sides and three angles of both triangles are equal.

The distance between two points on the coordinate plane is given as:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2) \\`

In triangle ABC:

`|AB|=√((2-8)^2+(6-4^2))=√(40) =2√(10)\\\\|AC|=√((5-8)^2+(0-4)^2)=5\\\\|BC|=√((5-2)^2+(0-6)^2 )=√(45)`

In triangle MNO:

`|MN|=√((1-7)^2+(2-4^2))=√(40) =2√(10)\\\\|MO|=√((4-7)^2+(y-4)^2)\\\\|NO|=√((4-1)^2+(y-2)^2 )`

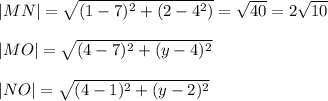
Since triangle ABC and triangle MNO are congruent, hence:

|AB| = |MN| = 2√10, |AC| = |MO| = 5, |BC| = |NO| = √45

`|AC|=|MO|=5\\\\√((4-7)^2+(y-4)^2)=5\\\\(4-7)^2+(y-4)^2=25\\\\9 +(y-4)^2=25\\\\(y-4)^2=16\\\\square\ root\ of\ both\ sides:\\\\y-4=4\\\\y=4+4\\\\y=8`

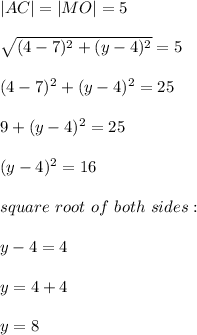
Hence O = (4, 8)