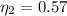Question

A source of heat at 1000 K transfers 1000 kW of power to a power generation device, while producing 400 kW of useful work. Determine the second law efficiency of the system, if the environment is at 300 K.

Answer 1

The value is
`\eta _2 = 0.57`

Step-by-step explanation:

From the question we are told that

The temperature of the heat source is
`T_s = 1000 \ K`

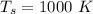
The amount of power transferred is
`P_s = 1000 \ kW = 1000 *10^(3) \ W`

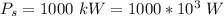
The work produced is
`W = 400 \ kW`

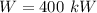
The temperature of the environment
`T_e = 300 \ K`

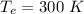
Gnerally the Carnot efficiency of the system is mathematically represented as

`\eta_c = 1 -(T_e)/(T_s)`

=>
`\eta_c = 1 -(300)/(1000)`

=>
`\eta_c = 0.7`

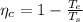
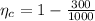
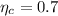
Generally the first law efficiency of the system is mathematically represented as

`\eta _1 = (W)/(P_s)`

=>
`\eta _1 = (400)/(1000)`

=>
`\eta _1 = 0.40`

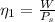
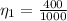
Generally the second law efficiency of the system is mathematically represented as

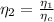
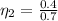
`\eta _2 = (\eta_1)/(\eta_c)`

=>
`\eta _2 = (0.4)/(0.7)`

=>
`\eta _2 = 0.57`