Question

Determine whether the function is even, odd, or neither. Then determine whether the function's graph is symmetric with respect to the y-axis, the origin, or neither.

f(x)=x³ - 2x

Answer 1

Answer: The function is odd and symmetric with respect to the origin.

Explanation:

A function is even if f(x)=f(-x), and odd if f(x)=-f(-x). If a function satisfies neither of these, it is neither even nor odd.

`f(x)=x^(3)-2x\\\\f(-x)=(-x)^(3)-2(-x)=-x^(3)+2x=-f(x)`

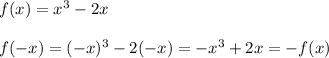
Therefore, the function is odd, and thus the function is symmetric about the origin