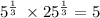Question

Select all which are equivalent to:
5^1/3 x 25^1/3

Answer 1

Note:

You missed adding the answer options.

But, I am solving the given expression to determine its equivalent so that you could get an idea and could easily determine all the options which would be equivalent to the result we would get.

Answer:

`5^{(1)/(3)}\:* 25^{(1)/(3)}=5`

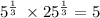
Explanation:

Given the expression

`5^{(1)/(3)}* \:25^{(1)/(3)}`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^mb^m=\left(ab\right)^m`

`5^{(1)/(3)}* \:25^{(1)/(3)}=\left(5* \:25\right)^{(1)/(3)}`

`=125^{(1)/(3)}`

`\mathrm{Factor\:the\:number:\:}\:125=5^3`

`=\left(5^3\right)^{(1)/(3)}`

`\mathrm{Apply\:exponent\:rule}:\quad \left(a^b\right)^c=a^(bc)`

`=\left(5^3\right)^{(1)/(3)}=5^{3* (1)/(3)}=5`

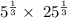
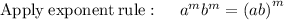
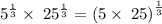
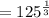
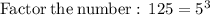
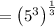
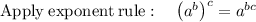
Thus,

`5^{(1)/(3)}\:* 25^{(1)/(3)}=5`