Question

Anna wants to purchase advertising space in the school newspaper. Each square inch of advertisement space sells for $3.00. She wants to purchase a rectangular space with length and width in the ratio 3:2 and she has up to $50.00 to spend. What are the dimensions of the largest advertisement she can afford to purchase?

(please explain how you got the answer and show me some work!!)

Answer 1

The largest advertisement she can afford has dimensions of 5 in x 10/3 in

Explanation:

Assume the dimensions of the advertisement are L and W.

The area of the advertisement is:

A = L.W

The ratio length/width is 3:2, thus the proportion is:

`\displaystyle (L)/(W)=(3)/(2)`

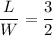
Thus:

`\displaystyle L=(3)/(2)W`

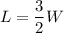
The area is:

`\displaystyle A=(3)/(2)W^2`

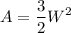
Since the square inch of advertisement space sells for $3, the cost for Anna to purchase it is:

`\displaystyle C=3\cdot(3)/(2)W^2`

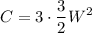
Simplifying:

`\displaystyle C=(9)/(2)W^2`

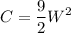
This cost can be a maximum of $50, thus:

`\displaystyle (9)/(2)W^2=50`

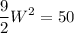
Multiplying by 2:

`9W^2=100`

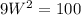
Solving for W:

`\displaystyle W=\sqrt{(100)/(9)}=(10)/(3)`

`\displaystyle W=(10)/(3)`

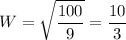
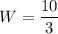
And

`\displaystyle L=(3)/(2)\cdot (10)/(3)`

L = 5

Thus the largest advertisement she can afford has dimensions of 5 in x 10/3 in