Answer:
The battery will last 2 hours
Explanation:
Inverse Proportion
Inverse proportion occurs when one value decreases and the other increases.
For example, more workers on a job would reduce the time to complete it. The number of workers and the time to complete the job are inversely proportional.
Martin's camping light has one switch that allows operating one, two, or three of the bulbs simultaneously.
The duration of the battery and the number of bulbs on are inversely proportional. When more bulbs are lit, the battery lasts less.
Assume the duration d and the number of bulbs b be related as:

We know the battery lasts 6 hours when only one bulb is burning, thus:
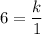
Thus: k = 6, and:
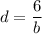
This equation is confirmed when b=2 and d=3.
If all three bulbs are on (b=3):

The battery will last 2 hours