Question

Steve determines that sides DK and BC are congruent. He also measures angle K and angle C and determines that they are congruent He concludes that the triangles are congruent by the SAS Congruence Theorem. Is Steve correct? If he is incorrect, which congruence theorem should Steve use? Explain your reasoning and show all of your work including measurement of angles and / o * r line segments .

Answer 1

See below

Explanation:

SAS requires two sides and the included angle to be congruent

Steve needs to measure sides EK and AC and if they are congruent, he can then complete his proof

Let's find the measure of EK and AC

• EC =
  `√((-4-4)^2 + (0-6)^2) = √(8^2 + 6^2) = √(100) = 10\\`
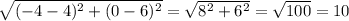
• AC =
  `√((-2 - 6)^2 + (9 - 3)^2) = √(8^2 + 6^2) = √(100) = 10`

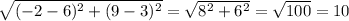
As we see EK = AC = 10, so the proof is complete