Question

Brianna has x nickels and y pennies. She has no less than 20 coins worth no more

than $0.80 combined. Solve this system of inequalities graphically and determine
one possible solution.

Answer 1

`y \ge 20 - x`

`y \le 80 -5x`

`(x,y) = (15,5)`

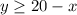
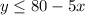
Explanation:

Given

`Nickels = x`

`Pennies = y`

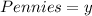
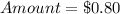`Amount = \$0.80` maximum

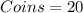`Coins = 20` minimum

Required

Solve graphically

First, we need to determine the inequalities of the system.

For number of coins, we have:

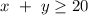`x\ +\ y\ge 20` because the number of coins is not less than 20

For the worth of coins, we have:

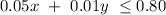`0.05x\ +\ 0.01y\ \le0.80` because the worth of coins is not more than 0.80

So, we have the following equations:

`x\ +\ y\ge 20`

`0.05x\ +\ 0.01y\ \le0.80`

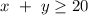
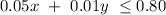
Make y the subject in both cases:

`y \ge 20 - x`

`0.01y \le 0.80 - 0.05x`

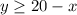
Divide through by 0.01

`(0.01y)/(0.01) \le (0.80)/(0.01) -( 0.05x)/(0.01)`

`y \le (0.80)/(0.01) -( 0.05x)/(0.01)`

`y \le 80 -5x`

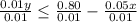
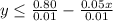
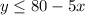
The resulting inequalities are:

`y \ge 20 - x`

`y \le 80 -5x`

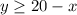
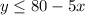
The two inequalities are plotted on the graph as shown in the attachment.

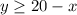`y \ge 20 - x` --- Blue

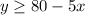`y \ge 80 -5x` --- Green

Point A on the attachment are possible solutions

At A:

`(x,y) = (15,5)`