Question

Find the lengths of the sides of rectangle ABCD shown on the coordinate plane. Suppose you double the length of each side. What would be the new coordinates of point C if the coordinates of point A stay the same​? Use pencil and paper to explain your reasoning.

Answer 1

(6, 8)

Explanation:

The rectangle ABCD has vertices at A(0,0), B(0,4), C(3,4) and D(3,0). The length of the sides is calculated using the distance formula:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

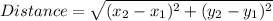
Therefore:

`|AB|=√((0-0)^2+(4-0)^2)=4 \\\\|BC|=√((3-0)^2+(4-4)^2)=3\\\\|CD|=√((3-3)^2+(0-4)^2)=4\\\\|AD|=√((3-0)^2+(0-0)^2)=3`

If the length of each side is doubled and point A stays the same. Let us assume that the new point of C is C'(x, y). Therefore C would be the midpoint of segment |AC'|:

`3=(0+x)/(2)\\\\x=6\\\\4=(0+y)/(2)\\\\y=8`

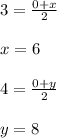
Therefore C'=(6,8)

The new coordinate of point C would be (6, 8)