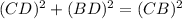Question

Given that CD¯¯¯¯¯¯¯¯ is a perpendicular bisector of AB¯¯¯¯¯¯¯¯, where D is on AB¯¯¯¯¯¯¯¯, how can you use the Pythagorean Theorem to describe the relationship of the side lengths of △ACD and △BCD?(1 point) (AD)2+(CD)2=2(CA)2 and (BD)2+(CD)2=2(CB)2 (CA)2+(CD)2=(AD)2 and (CB)2+(CD)2=(BD)2 (AD)2+(CD)2=(CA)2 and (BD)2+(CD)2=(CB)2 (AD)2+(CA)2=(CD)2 and (BD)2+(CB)2=(CD)2

Answer 1

what the fawk

Explanation:

Answer 2

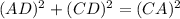`(AD)^2 + (CD)^2 = (CA)^2` and
`(CD)^2 + (BD)^2 = (CB)^2`

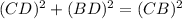
Explanation:

Given

Bisector: CD

of Line AB

Required

Apply Pythagoras Theorem

From the question, CD bisects AB and it bisects it at D.

The relationship between AB and CD is given by the attachment

Considering ACD

From the attachment, we have that:

`Hypothenuse = CA`

`Opposite = CD`

`Adjacent = AD`

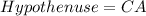
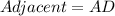
By Pythagoras Theorem, we have

`(AD)^2 + (CD)^2 = (CA)^2`

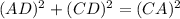
Considering CBD

From the attachment, we have that:

`Hypothenuse = CB`

`Opposite = CD`

`Adjacent = BD`

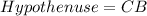
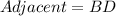
By Pythagoras Theorem, we have:

`(CD)^2 + (BD)^2 = (CB)^2`